Arithmetic Coding
In the world of dictionary coding and probability based encoding, the floating point weirdness that is arithmetic coding is a refreshing and surprisingly efficient lossless compression algorithm. The algorithm takes the form of two stages, the first stage translates a string into a floating point range and the second stage translates this into a binary sequence. Let’s take a look at how each stage works.
Stage 1: Floating Point Ranges
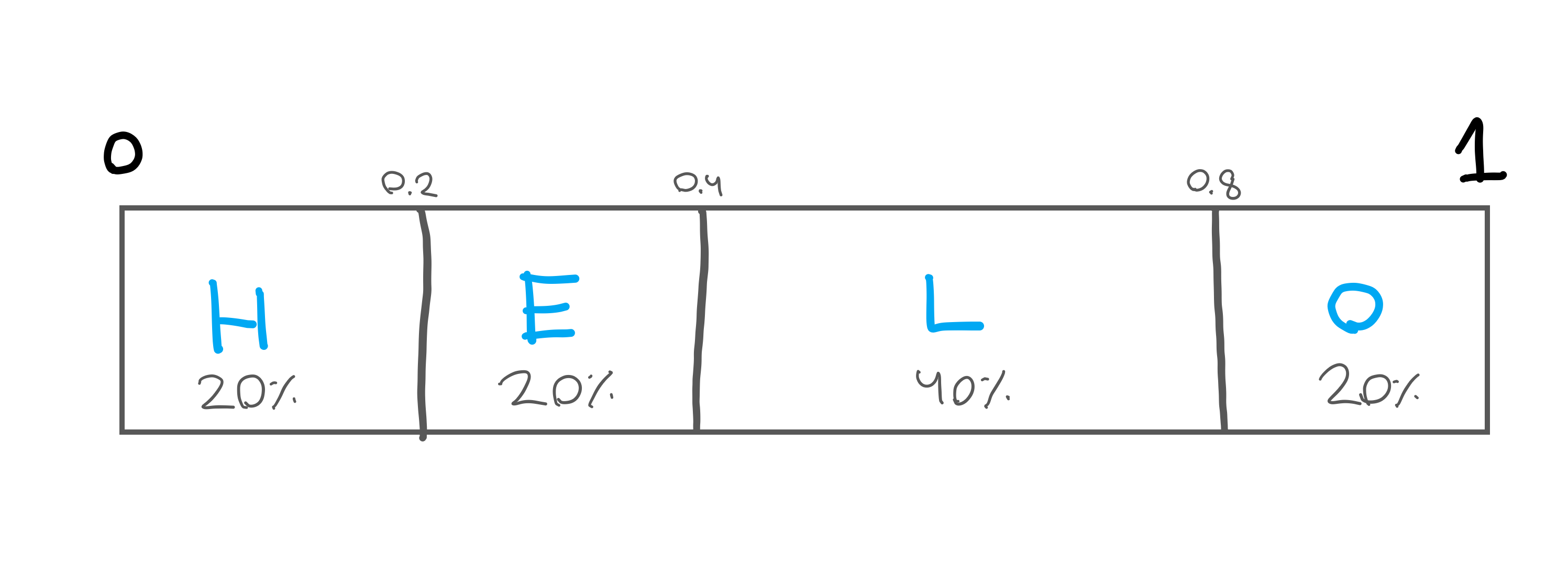
At a very broad level arithmetic coding works by taking a character and assigning it a frequency to a table. This frequency is then mapped to a number line between 0 and 1. So, if we have the character frequency table as shown below for the word “HELLO”, we would end up with our number line shown below.
| Character | Frequency | Probability |
|---|---|---|
| H | 1 | 20% |
| E | 1 | 20% |
| L | 2 | 40% |
| O | 1 | 20% |
To do the encoding, we need a floating point range representing our encoded string. So, for example, let’s encode “HELLO”. We start out by encoding just the letter “H”, which would give us the range of 0 to 0.2. However, we’re not just encoding “H” so, we need to encode “E”. To encode “E” we take the range from encoding “H”, 0 to 0.2, and apply our same frequency table to that. You can see this represented below.
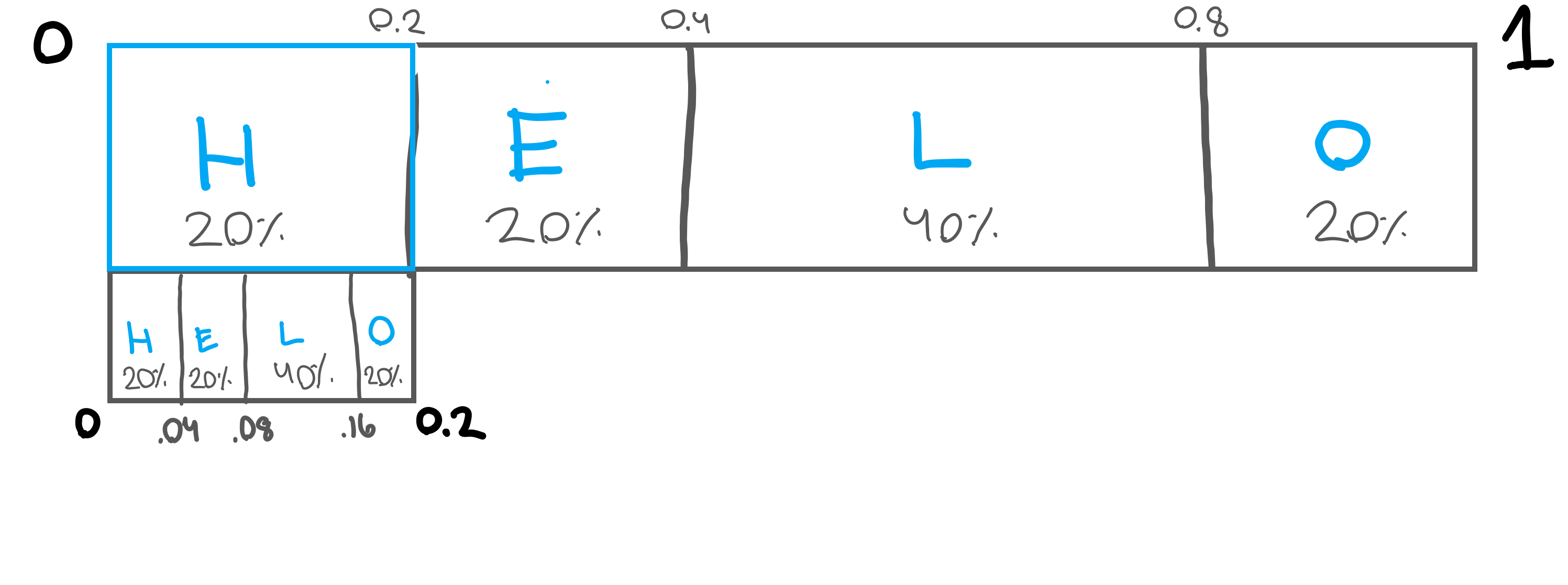
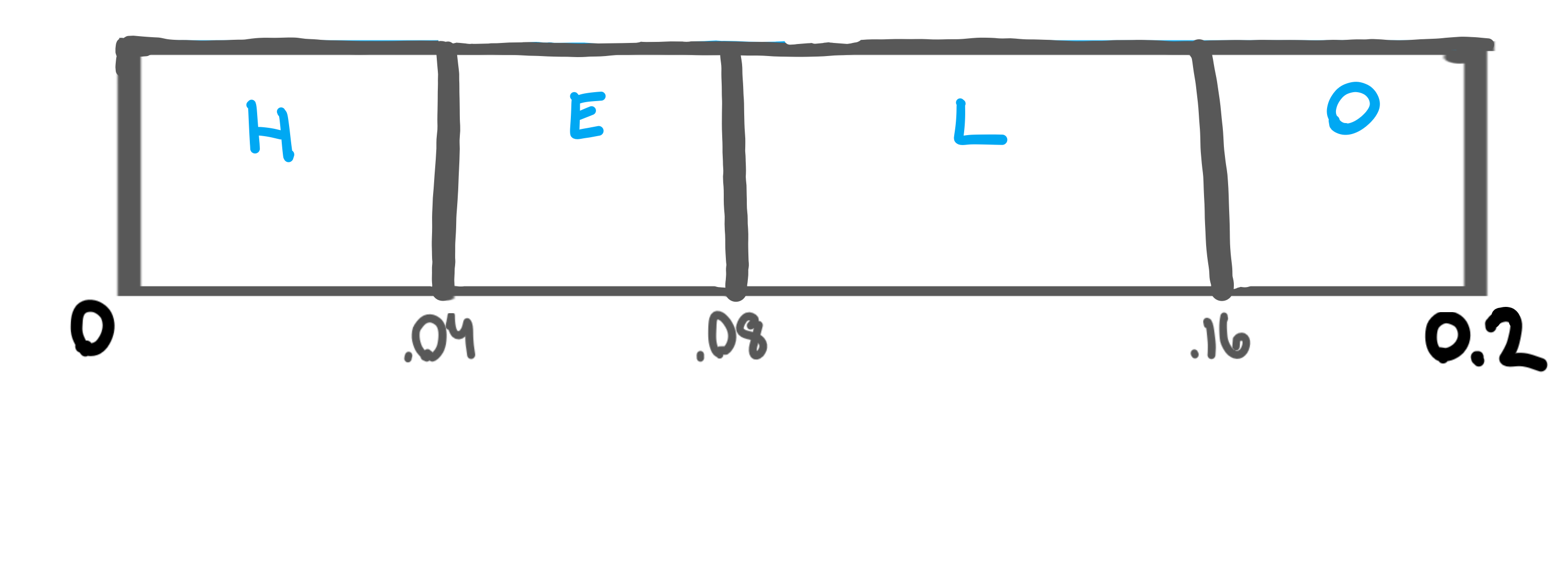
Blown up, you can see that we’re essentially copying the number line down, but fitting it within the range of 0 to 0.2 instead of 0 to 1.
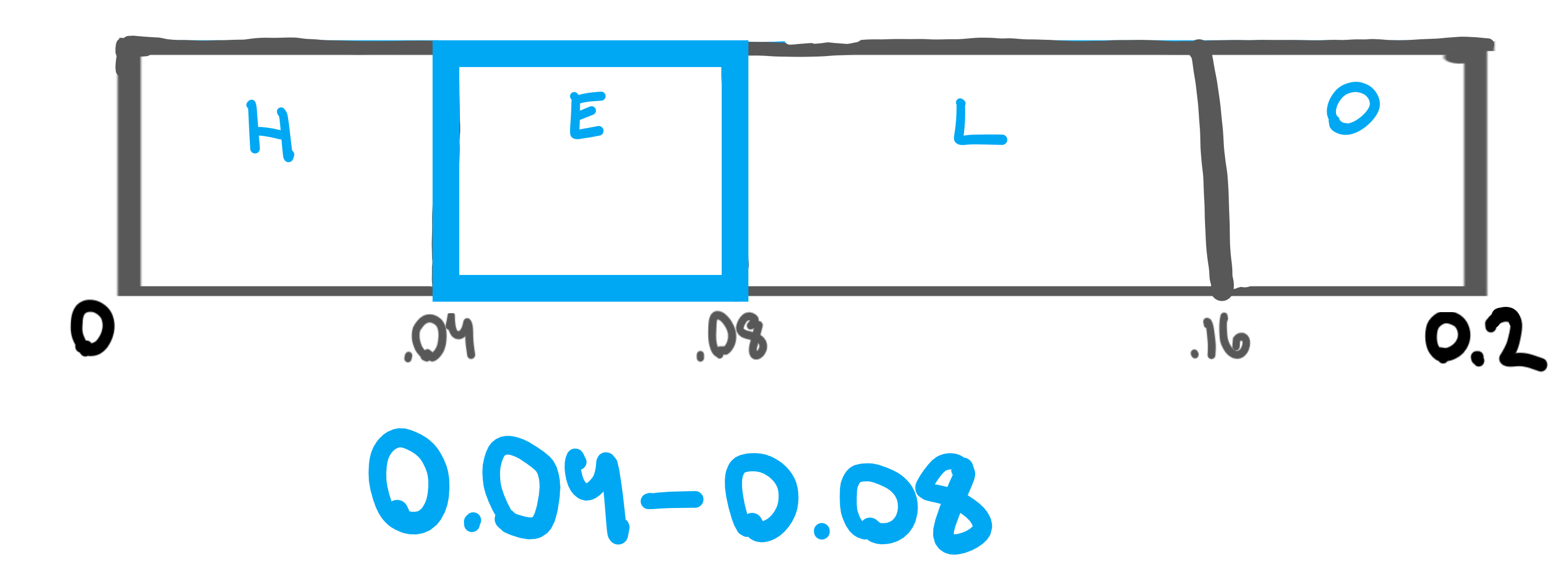
Now, we’ll encode the letter “E”, and we can see it falls within the range of 0.04 to 0.08.
As we move through this process, this copying of the number line and fitting it within the previous range continues until we encode our entire string. Though, if you’re familiar with floating point arithmetic in computers, you know that computers aren’t good with decimals, especially long ones. There are some workarounds to this, but generally floating point math is too inefficient or innaccurate to make arithmetic coding work quickly or properly for compression.
The answer to this issue is called finite-precision arithmetic coding, with the above approach of fitting the number line within a range known as the infinite-precision version because we (supposedly) have an infinite amount of precision.
Now if we continue this process, we get a range representing 0.06368 to 0.06496. The difference between these two numbers is just 0.00128, a big difference from the 0.2 difference when encoding just “H”. You can imagine that larger files will have an even smaller difference between the two ranges, spelling out the need for finite-precision arithmetic coding.
Stage 2: Binary Search
The next, and luckily final, stage is to run a binary search-like algorithm over the table to find a binary range that lays within our range from the first stage.
The way this works is actually quite simple. We take our number line from 0 to 1, and lay it out.

Then, we plot our range on the number line, and place our current target in the middle of the range: 0.5.
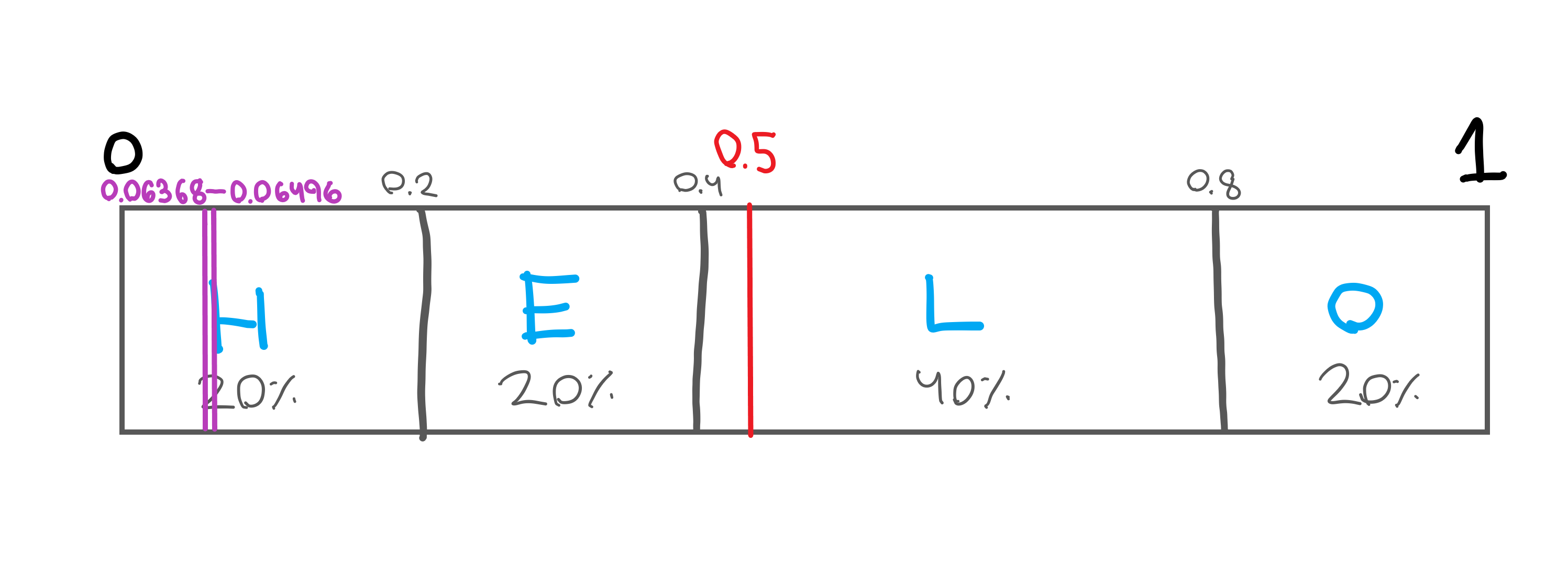
The trick is to see whether our range falls on the left or right side of our target (0.5). In this case, our range pretty clearly falls on the left hand side so we output a 0. If it fell on the right hand side we would output a 1.
Now here’s where things get interesting. We change the top end of our range from 1 to 0.5, so now we’re looking at the range from 0 to 0.5, with out target at 0.25 (0.25 is in between 0 and 0.5).
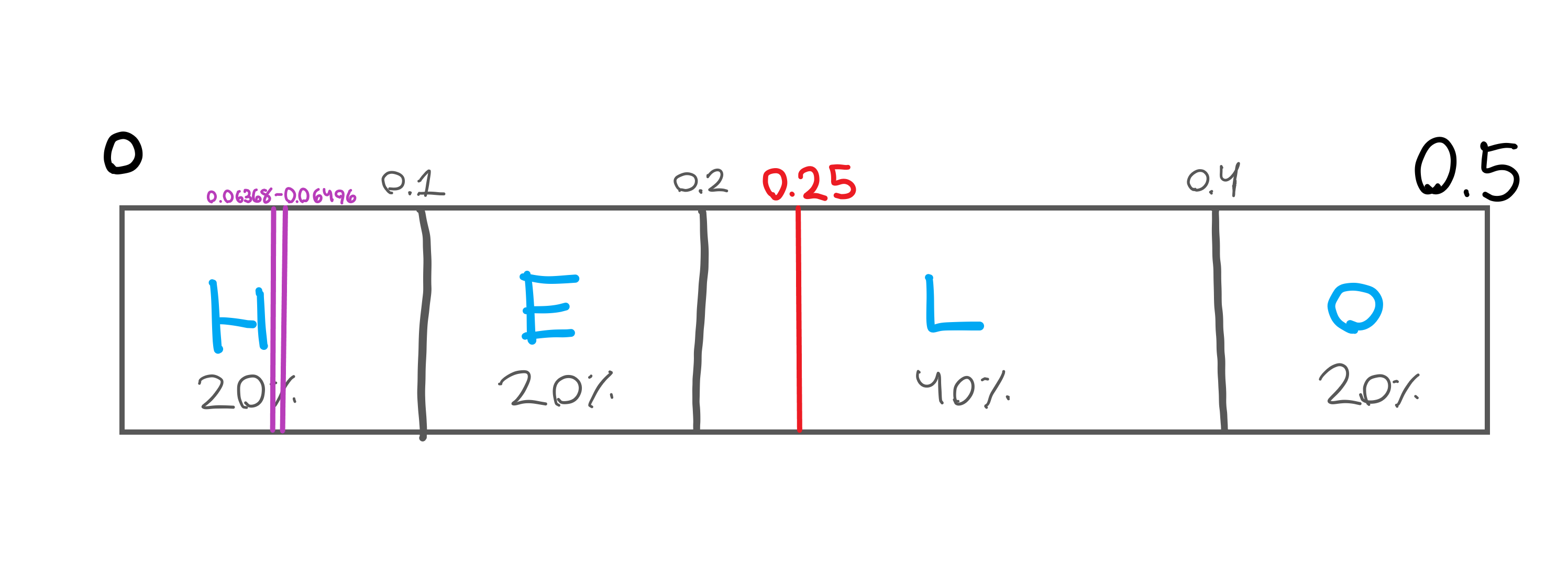
You can see the range moves closer to our target and the area between gets a little larger. It’s important to note we’re not changing the range, just looking at it magnified. Our range is still below 0.25 so we’ll output a 0 and repeat this process for the range of 0-0.25.
This continues until you’re left with a binary sequence that represents a target, just like the 0.5 and 0.25 from earlier examples, that lays within our encoded range from stage 1. This binary stream is the coded version (the compressed version) as we can use it to get back to the original string with the right frequency table.
Infinite vs. Finite Precision
Infinite precision is the process that we just went over with two stages. However as we saw, the more characters we encode, the smaller the difference between our range floor and ceiling gets. This means that as we encode more and more characters the top and bottom sections of the range will eventually meet and represent the same value because a typical 32-bit system cannot represent infinite precision. There are ways around this, such as increasing the size of the floating point number’s precision or using infinite precision, but these solutions don’t work for all data or are very inefficient respectively.
The harder solution is to combine these steps in one stage, which is called finite-precision arithmetic coding because it only requires a finite amount of precision to operate. This version works by encoding the first character, then immediately trying to see if the range falls above or below 0.5. If so, it will output the binary number representing which half it lays within and will “blow up” the range so that it doesn’t lose precision. There is also an important corner-case of encoding a “10” or “01” if the range lays within 0.25-0.75 which requires memory to be carried over from each encoding.
To put it simply, infinite-precision arithmetic coding is a simple and easy way to understand arithmetic coding while finite-precision arithmetic coding is more complicated but scalable and efficient.
Now unfortunately I can’t explain how to implement your own version of finite-precision arithmetic coding well enough to be comprehensive, so I’ll redirect you to a wonderful article by Mark Nelson that explains how to write an arithmetic coder with infinite and finite precision. There are also some wonderful online lectures by mathematicalmonk on YouTube that go into detail about finite-precision coding in a visual way. If anything in this article doesn’t make sense to you then I can’t recommend mathematicalmonk’s YouTube lectures and Mark Nelson’s article. Arithmetic Compression from Compressor Head on YouTube is also a great and enjoyable primer on the topic.
Adaptive Arithmetic Coding
One last variation of arithmetic coding worth mentioning is the idea of adaptive arithmetic coding. This version works in mostly the same way as typical arithmetic coding except that rather than building a frequency table from the source, it builds the frequency table as it encodes each character.
This means if you were encoding “HELLO”, it would start with “H” representing 100% of the table. When it encoded the “E”, it would update the frequency table so “H” would represent 50% of the table and “E” representing the remaining 50%. This concept allows arithmetic coding to adapt to the content as it’s encoding which allows it to achieve a higher compression ratio.
Resources
If you’re interested in learning more about arithmetic coding, check out these great resources:
- Mark Nelson - Data Compression With Arithmetic Coding
- Arithmetic Compression from Compressor Head
- mathematicalmonk - Arithmetic Coding